Dirichlet过程是一个常用于非参数模型的随机过程,对于随机过程的性质可以类比于Gauss过程。它是一个定义在分布上的分布,也就是说每一个Dirichlet过程的样本都是一个分布。从Dirichlet过程中抽样的分布是离散的,但是不能用有限个参数表示这样的过程,因为在每个点(无穷维)都可以定义采样点,因此这是一个非参数的模型。
我们考虑下面这样一个hierarchical的模型:

一个Dirichlet distribution是定义在K维的单纯形上面的分布:
我们说具有以下密度函数形式的称为Dirichlet 分布:
Dirichlet 分布的性质
1.可加性:
若有:
2.累乘性质:
那么Dirichlet Process可以看成无穷维度的Dirchlet分布:

Dirichlet process
狄利克雷过程是定义在分布(概率测度)上的分布,对于任意base distribution H的有限划分,有
其中
注意到Dirichlet是离散的分布,分布函数是一个阶梯函数。

Dirichlet 后验
假设我们从Dirichlet过程F中采样出来了
注意到后验分布的基分布是关于原来先验的基分布H和经验分布
生成Dirichlet Process
Blackwell-MacQueen Urn Scheme
生成过程:
每一个
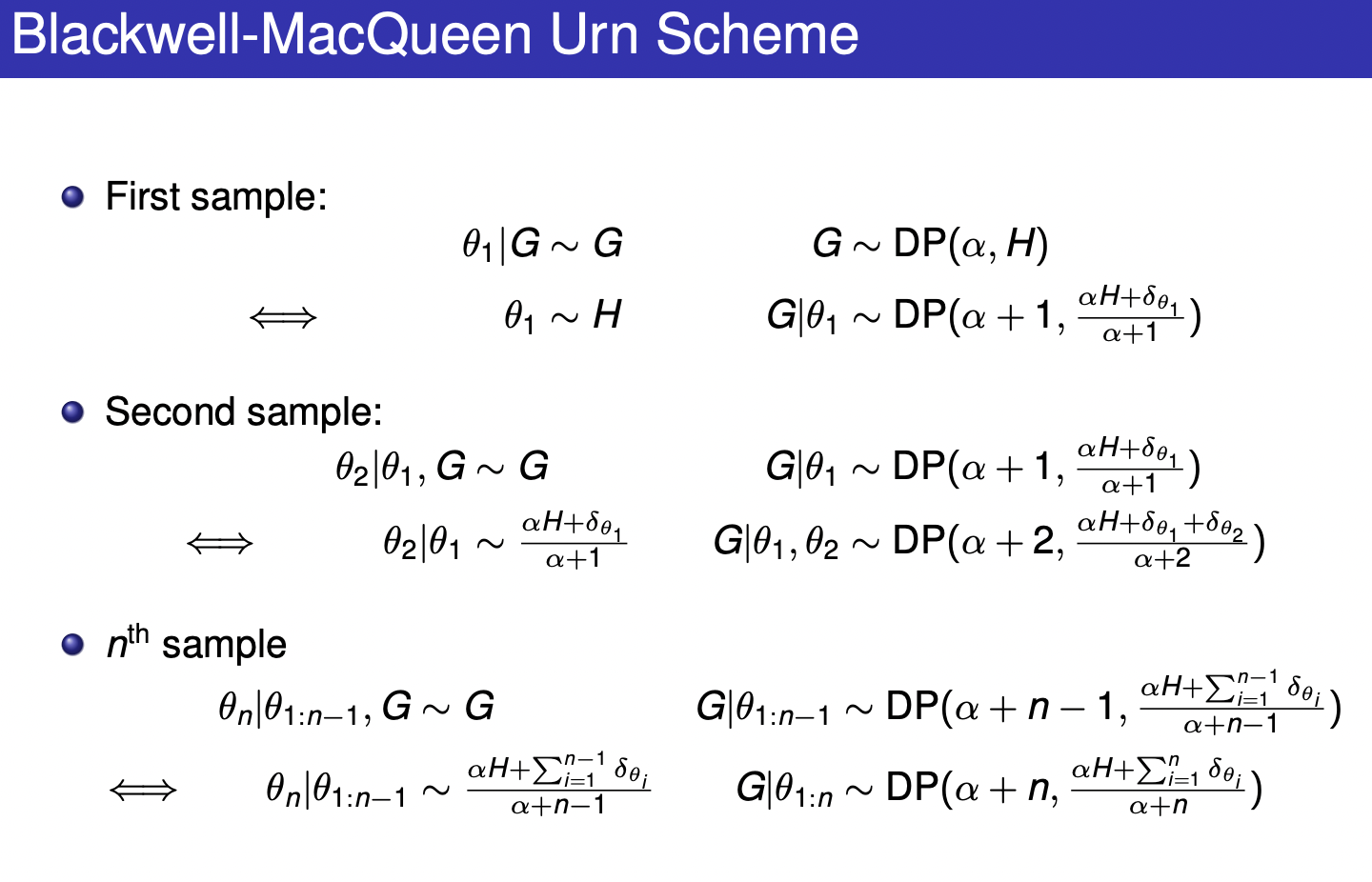
Stick-breaking 生成



考虑一根长度为1的棍子,我们在
参考网址:
1.Dirichlet Process tutorial(pdf)
2.Dirichlet Processes: Tutorial and Practical Course
4.Introduction to the Dirichlet Distribution and Related Processes